Leonardo Di Vinci, (1452 – 1519) is widely regarded as the quintessential renaissance man, a genius, a polymath, a master painter, sculpture, engineer, inventor and much, much more. He is considered to have possessed one of the greatest minds in human history and to be one of the most creative and talented beings that ever existed.
His painting known in English as the Mona Lisa and in Italian as La Giaconda, is arguably the most famous and popular painting in the world and for all history.
Yet, what made this man so impossibly talented across so many artistic fields? Could the secret, at least in part, to his unfathomable talent lie in another of his passions, mathematics?
Mathematics was seen by many of the world’s great thinkers at the time of Di Vinci as part philosophy, part science and very possibly possessing the keys to unlocking the mysteries of the universe. One area where math and art merged was something known as the ‘Divine Proportion’, a ratio which was considered to be natural perfection and could be employed in art to render perfect compositions.
Di Vinci is known to have studied the ‘Divine Proportion’ even illustrating a book on the subject for his friend Luca Pacioli. Many art scholars believe that Di Vinci used this divine ratio in many of his paintings and sculptures and whilst hotly contested, it has been suggested by a great many art historians and specialists in the fields of geometry and mathematics that his most famous work does conform to this notion that there is a divine set of numbers that can be used like magic to deliver the perfect composition. In Di Vinci’s case, deliver to the world its most famous painting.
Fibonacci, (aka: Leonardo of Pisa) was born around 1170, his father was –according to certain versions of history- a shipping clerk nicknamed Bonaccio, which is said to have been a nickname of sorts meaning ‘Simpleton’, thus Fibonacci’s name meant, ‘Son of a Simpleton’.
The young Fibonacci traveled extensively throughout North Africa with his father and in Bejaia, Algeria he learnt the Hindu/Arabic numerical system. Realizing the superiority of this numerical system Fibonacci traveled throughout the Mediterranean studying under the leading Arab mathematicians of the age. He returned to Pisa in 1200 and by 1202 was ready to publish his magnum opus, the ‘Liber Abaci’, (Book of Abacus). This book introduced the western world to the Arabic numeral system and it is entirely possible that if not for his work, we could all still be using the much less efficient Roman numerals.
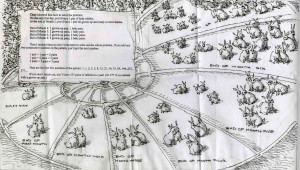

Ever heard of the term to ‘Breed like Rabbits’? Fibonacci -as a sort of medieval joke- set out in the Liber Abaci to show just what it meant to breed like rabbits using a numbers sequence he had learnt from ancient Indian mathematics. He posed a question: Say you had an idealized pair of rabbits who gave birth every month to a new rabbit, also submit that the rabbits born were always a male and a female and allow that none of the rabbits ever died and each began to breed after one month; after one year, how many pairs of rabbits would you have?
Fibonacci set out a series of numbers in sequence to demonstrate the outcome: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, with each new number representing the total sum of the previous two numbers added together.
This series of numbers is now immortalized as the ‘Fibonacci Sequence’ and is considered the most efficient numerical sequence in the universe, it turns out it is so efficient that it occurs all throughout nature and in all manner of creation.
Fibonacci numbers appear everywhere, from the leaf arrangement in plants, to the pattern of the florets of a flower, the bracts of a pinecone, the shoots of a grapevine, or the scales of a pineapple. The Fibonacci numbers occur in the growth of every living thing, including a single cell, a grain of wheat, a hive of bees, a seashell and even all of mankind.
The numbers reoccur in nature because it turns out to be the most efficient way for things to grow; in the seeming randomness of the natural world we discover numerous examples of the Fibonacci sequence. Today Fibonacci numbers appear in computer algorithms and in stock market and economic strategies.


An interesting aside, is to flip the Fibonacci Sequence and go back in time, starting in the present with a single human being instead of a pair if rabbits. Now let’s say the human is of English decent, he is the product of one mother and one father, who in turn are the product of their four parents, who were created by the union of eight more people, who came from sixteen more and so on back through the generations and back through time. Once you reach somewhere around the reign of the last Plantagenet king you realize there were more people involved in the creation of this one modern day human than the entire population of the country at that time.
Thanks to work by such luminaries as Joseph Chang of Yale, Peter Ralph of the University of Southern California and Graham Coop of the University of California two name a few; we learn that you only need to go back about six hundred years to find that every living European man woman or child shares a common ancestor, or more specifically, many common ancestors. This can be taken back even further in time to identify that every single person on the planet is related to a single common ancestor, which is estimated to be only about 3,500 years ago.

Whilst we are dwelling on the past, let’s go back for a minute to the Fibonacci numbers. The mathematician and astronomer Johannes Kepler, (1571-1630) proved that an ancient Greek ratio is the limit of the ratio of consecutive Fibonacci numbers he described this ratio as a “precious jewel”: “Geometry has two great treasures: one is the Theorem of Pythagoras, and the other the division of a line into extreme and mean ratio; the first we may compare to a measure of gold, the second we may name a precious jewel.” These two treasures are combined in the Kepler triangle.
Now here is where Fibonacci numbers get really interesting, if you divide a Fibonacci number, (especially the big numbers) with the number that precedes it, you will get the same ratio, reflected as a number, that number is 1.618….ad infinitum.
Long before the time of Fibonacci, the ancient Greeks understood the significance of this ratio; they named it the ‘Golden Ratio’. The Golden Ratio is what we call an irrational number: it has an infinite number of decimal places and it never repeats itself.
Take a series of squares that in size correspond to a sequence of Fibonacci numbers, if you put them all together they will form a rectangle, known as the ‘golden rectangle’; if you then run a line through each square in the rectangle, connecting at the corners, you will end up with a spiral whose ratios equal the golden ratio at each juncture. This golden spiral will correspond to the spirals in a nautilus shell, a snail shell, the cochlea of the inner ear, a pine cone, a seedpod, examples of this golden ratio appear again and again in nature and throughout all that is known.
The spirals of galaxies confirm to the golden ratio, the rings of Saturn, the triangles of the great pyramids are proportionate to the golden ratio, the anatomy of dolphins, humans, skeletal structures, blood vessel systems; in fact all living beings conform to the golden ratio. The one thing that all life has in common is DNA. Instead of centimeters or inches, angstroms are the unit of measure used for DNA, a full segment of DNA is roughly 21 angstroms wide & 34 angstroms long for each full cycle of its double helix spiral. Twenty one and Thirty Four are consecutive Fibonacci Numbers; if you look at the grooves as spirals of the double helix strand it is proportionate to the Golden ratio.
‘Some of the greatest mathematical minds of all ages, from Pythagoras and Euclid in ancient Greece, through the medieval Italian mathematician Leonardo of Pisa and the Renaissance astronomer Johannes Kepler, to present-day scientific figures such as Oxford physicist Roger Penrose, have spent endless hours over this simple ratio and its properties. But the fascination with the Golden Ratio is not confined just to mathematicians. Biologists, artists, musicians, historians, architects, psychologists, and even mystics have pondered and debated the basis of its ubiquity and appeal. In fact, it is probably fair to say that the Golden Ratio has inspired thinkers of all disciplines like no other number in the history of mathematics.’
Mario Livio, the Golden Ratio: The Story of Phi, the World’s Most Astonishing Number


The Parthenon in Greece confirms to the golden ratio however, the golden ratio has been employed by architects, designers, painters and sculptures since well before the time of the Ancient Greeks; the great pyramid of Giza, believed to be four thousand, six hundred years old conforms to the golden ratio., the great mosque of Kairouan conforms to the golden ratio.
The exact origins of the Golden Ratio are sketchy, Greek mathematician Pythagoras, (born around 570 BCE) in his Pythagoras’ Theorem was a starting point to unlocking its mystery, his followers, known as Pythagoreans, had a pentagram as their symbol which itself represents the golden ratio.
Greek sculptor, painter and architect Phidias, (480 – 430 BCE) is regarded as one of the greatest sculptors in history, his statue of Zeus at Olympia was considered one of the Seven Wonders of the World. He created Athena Parthenos in Athens and he is believed to have been in charge of other Parthenon sculptures. Many art historians conclude that Phidias made meticulous use of the golden ratio in proportioning his sculptures
Euclid (c. 325–c. 265 BC), in his Elements, gave the first recorded definition of the golden ratio, which he called, “extreme and mean ratio”.
De divina proportione, written by Luca Pacioli in Milan in 1496–1498, published in Venice in 1509, features 60 drawings by Leonardo da Vinci, some of which illustrate the appearance of the golden ratio in geometric figures. Starting in part with the work of Leonardo da Vinci, this architectural treatise was a major influence on generations of artists and architects.
Mozart divided a striking number of his sonatas into two parts whose lengths reflect the golden ratio, though there is much debate about whether he was conscious of this. In more modern times, Hungarian composer Bartok and French architect Le Corbusier purposefully incorporated the golden ratio into their work.


The Sacrament of the Last Supper (1955): The canvas of this surrealist masterpiece by Salvador Dali is a golden rectangle. A huge dodecahedron, with edges in golden ratio to one another, is suspended above and behind Jesus and dominates the composition.
French mathematician, Henri Poincare, (famous for his mathematical conundrum, ‘Poincare’s Conjecture’, which was part of the Millennium Prize for mathematics and took almost 100 years to solve) taught the properties of the golden ratio to Juan Gris, who developed Cubism featuring golden ratios.
Even today, the golden ratio is in human-made objects all around us. Look at almost any Christian cross; the ratio of the vertical part to the horizontal is the golden ratio. To find a golden rectangle, you need to look no further than the credit cards in your wallet or, look at a great many logos of some of the world’s most famous brands.
It wasn’t until the 1900′s that American mathematician Mark Barr used the Greek letter phi (Φ) to designate this proportion. By this time this ubiquitous proportion was known as the golden mean, golden section and golden ratio as well as the Divine proportion. Phi is the first letter of Phidias, who used the golden ratio in his sculptures, as well as the Greek equivalent to the letter “F,” the first letter of Fibonacci. Phi is also the 21st letter of the Greek alphabet, and 21 is one of the numbers in the Fibonacci series.
The Mona Lisa is an enigmatic figure, she draws people in, they stare and wonder and they keep coming to the Louvre in Paris every day of every year to stare in awe and amazement, it has been called the most visited, written about, sung about and parodied painting in history. Today, this five hundred year old painting has an estimated insurance value of over 750 million US dollars, making it the most expensive painting in the world. The question still remains today, was Leonardo Di Vinci painting by numbers?